Alex Haslehurst

Machine Learning From Scratch

29 July 2025
Alex Haslehurst
32 min read

For modern (laptop scale) machine learning, it is usual to depend on a library such as PyTorch. These libraries have massively lowered the barrier to entry into machine learning by abstracting away the mathematics behind it, having you running big models on your GPU with little effort. This is great as anyone with basic Python programming skills and the ability to follow a tutorial (or effectively prompt an LLM), can get started with machine learning. I've had a play with PyTorch but left feeling I'd learned more of the abstraction than the underlying concepts.

As a learning exercise and of course for fun, I decided to go back to basics and implement my own machine learning from scratch.

First I needed a target, preferably a game, since... games are fun. I've been making low level games in Rust: I learned Rust to make games!. They're actually perfect for this project as:

There is no engine (like Unity or Godot) so I don't have to worry about bindings or non-machine learning relevant baggage getting in the way.

I have direct access to the game loop so integrating an agent into the game is dead easy:

fn game_loop() {
    let mut game = Game {};
    let mut agent = AiAgent {};
    loop {
        // let input = read_human_controls(); ← humans need not apply
        let input = agent.act(&game); // ← the agent is playing instead
        update_game_state(&mut game, input);
        draw_game(&game);
    }
}

fn game_loop() {
    let mut game = Game {};
    let mut agent = AiAgent {};
    loop {
        // let input = read_human_controls(); ← humans need not apply
        let input = agent.act(&game); // ← the agent is playing instead
        update_game_state(&mut game, input);
        draw_game(&game);
    }
}

Rust is so fast that I don't need perfectly optimised code for it to be performant.

I chose a Tetris clone rustris for this project.

The game of Tetris is played with a tetromino that falls from the top of a board. When the tetromino touches the bottom of the board, or the stack, it will enter a lock state, where after some timeout and without action, it will lock into place and become part of the stack. The stack is cleared by arranging lines. The maximum number of lines that can be cleared in a single move is 4, which is called a Tetris. Points are added for various actions and outcomes in the game. The game is lost when the stack reaches the top of the board. It is expected that every game will eventually be lost, games are classified by the number of lines cleared and the total points scored.

Every tetromino has a name:

Name	Tetromino
`O`
`Z`
`S`
`T`
`L`
`J`
`I`

First I need to design the API of the agent. A Tetris playing agent will consume game state to produce actions:

Naively, and with a cluster of GPUs, we would provide the model with raw board state. The Tetris board is 10x20 which is 2²⁰⁰ = 1.6 * 10⁶⁰ distinct states. Whilst the model having access to this massive amount of raw state would provide the best chance of complex strategies emerging, this scale is unfortunately out of scope. I am looking for something more laptop scale than RTX 5090. I am also much more interested in developing the model from scratch than having something cutting edge.

So I decided to pre-optimise the game state into "features".

Feature	Description
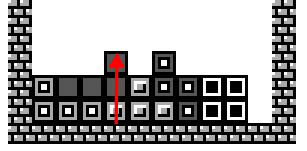	Maximum Stack Height e.g. 3
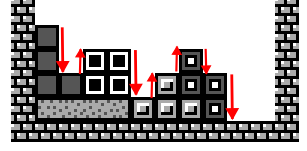	Roughness e.g. 2+1+2+1+1+1+2 = 10 To express the "flatness" of the stack. I played a LOT of Tetris for this project and realised that 5/7 Tetromino have a flat side so the optimal stack shape is as flat as possible.
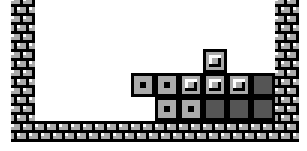	Open Hole One or more empty blocks with a stack block above but not on either side. Can be filled by sliding a Tetromino.
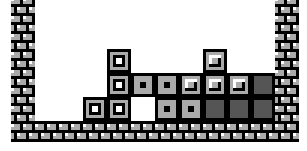	Closed Hole One or more empty blocks completely surrounded by stack or walls. Can only be filled by removing stack blocks above.
	Pillar A gap 3 or more blocks tall that can only be filled with an I Tetromino.

I take the delta of each feature for each available tetromino placement. I think this is important as the model will learn much better when for every action it takes, no matter the existing state of the board, the input parameters will change at the same scale. E.g. without taking the delta, if there are 15 holes already and placing a tetromino creates another hole, then the hole feature will change by an amount that is 15x less than what would have been observed on an empty board.

I also tell the model when:

It has covered a hole.
It has cleared a line.
It has cleared a Tetris (4 lines).
Tetromino altitude - the max y-coordinate of the final position of the tetromino.

Another scaling issue applies to how actions are interpreted from the model output. Tetris uses a spatial control scheme Left, Right, Rotate. Humans can naturally interpret a desired placement, for example slotting an I tetromino into a gap in the stack, as a series of Left, Right, Rotate commands.

If we expect a model to generate output like this, it must be expected that it has to dedicate significant resources to learning the spatial nature of the game. I am sure that I have a low chance of pulling off something sophisticated enough to handle spatial reasoning. Instead, I will use an algorithm that, given the current state of the game, generates all possible placements available and provides them to the model summarised by their features.

The move search algorithm is a breadth-first search over all possible tetromino placements. It explores all possible placements of the current tetromino by taking every valid move that results in a new final (locked) position. This borders on brute-force but is feasible as the number of placements is limited by the board size. There are only 17 possible placements of the I tetromino on an empty board for example.

The move search algorithm is then run again with the final positions of the first run as the new starting positions. This is to explore any positions that can only be found by moving the tetromino during the lock phase, for example sliding a tetromino left or right into an open hole.

This entire process is run once for the current tetromino and then again for the 'held' tetromino.

At this point, I was ready to implement a model. I had a load of code that was unit tested (of course) but not integrated, so I chose to start with the simplest possible model, a linear function over all the features.

Q = P_1\delta StackHeight + P_2\delta Roughness + P_3\delta OpenHole + P_4\delta ClosedHole + P_5\delta Pillar

Where Q is the quality of the move and P are the parameters to be learned.

It works surprisingly well!
The model parameters are transparent, they can easily be sense checked e.g. I expect holes to be a good indicator of bad play, so I therefore expect the hole coefficient to be highly negative.
The model is incapable of learning complicated, non-linear strategies e.g. play safe when the stack is high.

With a simple model in place, I was ready to implement the agent. The agent, running directly in the game loop, will:

With the game state, run the move search algorithm to get all possible placements
Use the model to qualify each placement
Take game actions to execute the best placement (e.g. left, rotate, drop)

The linear model only has 10 parameters to learn, so I could actually hand-pick them and get a fairly decent result. The model will get more complex though so let's do some machine learning anyway.

The natural choice for a linear model would be linear regression. Linear regression is a supervised machine learning technique that relies on labelled data to (basically) plot a line of best fit for each statistically significant component. Think y = mx + c from GCSE.

I used to work in credit reference so am pretty familiar with the technique (your credit score is literally just a linear regression over your credit reference data). For supervised learning, I needed to label the data. My options are:

Record my gameplay, labelling my actions as good moves. This, whilst maybe fun to achieve, would mean that the model would be biased towards my decisions rather than the actual 'best' decisions. I have played a LOT of Tetris, but I am not a Tetris master, I probably make hundreds of mistakes in each game and this bias would be learnt by the model.
Collect professional Tetris gameplay, labelling professional player actions as good moves. There are high quality recordings of professional Tetris gameplay available online. I would have to write a tool to extract the game state and actions from the video. Whilst I think this could work well, it would be a lot of work, so I have put it aside for now.

Also: even professionals make mistakes.

Reinforcement learning is a machine learning technique where an agent is free to act in the environment and is given a reward, positive or negative, for each action it takes. The model learns to choose the actions that maximise cumulative reward.

I was not overly enthusiastic about reinforcement learning for this project:

I did not want to define a detailed reward function as this risks influencing behaviours based on preconceptions. E.g. if I defined a reward for clearing lines that was maybe slightly too high, then the model would learn to clear lines at the expense of all other strategies.

I briefly considered a broader reward function that worked retrospectively. E.g. when a game is lost, all placements leading up to the final placement before loss are penalised, whereas placements leading up to a Tetris clear are rewarded. I decided to skip this for now though as it seemed like it would be a mess of hyperparameters and the algorithms weren't massively clear to implement from scratch. I will definitely come back to this later though, maybe as an optimisation step for a model pre-trained with unsupervised learning.

Unsupervised learning is a machine learning technique used to find patterns or structure in unlabeled data. It effectively searches for a point in the multidimensional space over the model parameters that maximises some reward function.

I decided to go with this approach to start because:

Tetris has a native reward function that is a good fit: the game score.
This technique requires a lot of data but my Rust implemented game can simulate multiple hours of gameplay per second. My laptop won't be happy with it, but it shouldn't be a problem playing many thousands of games over a typical training run.
The unsupervised algorithms are fun to implement e.g. a genetic algorithm is based on evolution.

A genetic algorithm is an unsupervised learning technique, mimicking the process of evolution. It acts like a search heuristic for maximising some reward function over the model parameters.

Survival of the fittest: only the best (fittest) solutions will survive to have a chance of selection.
Selection: the fittest solutions are weighted by their fitness and merged into new solutions.
Mutation: some solutions are randomly changed to create new solutions.

Like real evolution, it has no concept of gradient decent, it is literally picking random solutions over multiple generations and mutating them in a process that over time (hopefully) causes a "population" to converge on an optimal solution.

In Tetris, the next tetromino is randomly chosen from a "bag" containing all 7 shapes. Once the bag is empty, the tetromino shapes are placed back in the bag and the bag is shuffled. This makes a Tetris playing model unstable, which is especially an issue for unsupervised learning algorithms, which rely on (mostly) random chance to find an optimal model. If the models are unstable, then training is less likely to converge on something optimal. TLDR; the randomness of the game means that the quality of the optimal model can deteriorate over time. Whereas we want the opposite!

To solve this, I first seed the random number generator with a random (time based) value, then I rotate the seed every 100 generations. This gives the training algorithm chance to converge on a model for a single deterministic game. My hope is that over time, the most generally optimised models will be selected and the training algorithm will converge on a model that is stable across many games.

I trained the linear model with a genetic algorithm for 700 generations of 1000 models each.

Here are the coefficients of the linear model after training:

As expected, the model has learned that:

Covering a hole is the worst thing you can do as it makes clearing the hole more difficult.
Closed holes are bad.
Open holes are bad but not as bad as closed holes, since you can sometimes fill them with a sliding tetromino.
Pillars are bad as they can only be filled with an I tetromino.
Tetris clears are good.
All the other coefficients are in a fine balance as they all interact with each other. E.g. you would imagine that clearing a line would be a good action to take, but the model actually applies a small penalty for a line clear, which seems weird in isolation. This looks to be offset by a small preference for a taller stack. Maybe this combination of coefficient values work better for some stack arrangements than others.

Here's the plot of the best score over 700 generations:

Observations:

You can see the dips in quality at every 100th generation, this is when the random seed is changed.
The model seems to stagnate before each dip.
After the dip, the model performance often recovers to a greater level than the previously stagnated performance. This must mean that the model is learning a more generalised strategy that is not biased towards a particular seeded game.
The model converges on a score of around 16 million points, which is pretty close to the current classic NES world record of 16.7 million points.
The trend looks logarithmic i.e. longer training runs probably won't improve the performance of the model much more.

With the linear model working, it's parameters sense checked, the bugs fixed in the genetic algorithm and the agent proven, I was ready to try a more complex model. I needed something non-linear that could potentially learn complex strategies, so I went with a neural network. To keep the existing, proven agent structure, I needed the network to be a direct replacement for the linear model, with the exact same inputs and outputs. The input layer must have one neuron per game feature and the output layer must have a single neuron; the quality of the move.

neural network

The whole point of this is to provide a model architecture allowing for non-linear behaviour to emerge, so:

I give the model the delta of each feature AND the absolute values, so it has the context of the current action, plus the global state of the game available.
I use multiple hidden layers to allow the model to learn complex relationships between the features.
I use a non-linear activation function, the sigmoid function.

The neural network topology I settled on is:

Input layer with 20 neurons
2 fully connected hidden layers with 20 neurons each
Fully connected output layer with 1 neuron

This totals to 1,281 parameters. For reference GPT-4 has 1.8 trillion parameters, so this is a very small model.

Of course, I could have used a library here like burn (remember I'm using Rust so PyTorch is not a practical option) but I wanted to implement a neural network from scratch, as a learning experience.

In my model, a neuron is a mathematical function that:

Applies a weighted sum over input values, mostly the results from other neurons.
Adds a constant value to the result, so that an activation bias is possible.
Passes the result through an activation function, which introduces non-linearity into the neuron.

Therefore, each neuron has two sets of parameters:

A weight for each input value.
A single bias value.

Neurons are arranged in layers:

The input layer, which takes the model input parameters.
One or more hidden layers, which allow the model to build increasingly complex abstractions over the input parameters.
The output layer, which produces the model output.

The networks I have implemented are fully connected feed-forward networks. That means that every neuron in one layer is connected to every neuron in the next layer. There are decent strategies for learning a more optimal network topology, such as NEAT (NeuroEvolution of Augmenting Topologies), but I decided to let the training process decide which connections are not important. In training, the weight of useless connections should tend towards 0, which effectively removes them from the model.

This is actually a simplification as it means that I can implement the network with A-level grade matrix multiplication. For illustration, given a simple network with two layers:

neural network

Then the output of the network can be expressed as a matrix multiplication of the weights and inputs, plus the biases, all passed through the activation function:

\begin{bmatrix} x \\ y \end{bmatrix} = \sigma \left( \begin{bmatrix} a_x & b_x & c_x \\ a_y & b_y & c_y \end{bmatrix} \otimes \begin{bmatrix} a \\ b \\ c \end{bmatrix} + \begin{bmatrix} x_{\text{bias}} \\ y_{\text{bias}} \end{bmatrix} \right)

Doing some A-level homework, this can be multiplied out into components:

x = \sigma(a_x a + b_x b + c_x c + x_{\text{bias}}) \\ y = \sigma(a_y a + b_y b + c_y c + y_{\text{bias}})

Ignoring transformers and the attention mechanism, modern LLMs are literally this but turned up to 11. They're using trillions of parameters over hundreds of layers but at their lowest level, they are simply tensor (n-dimensional) multiplication. It is amazing that reasoning seems to emerge from something so mathematically simple.

It is usual to train a neural network with a supervised learning technique such as backpropagation. I did implement backpropagation to test my neural network implementation, but the technique is not applicable, as I lack good quality labeled data.

Since the neural network model is a direct replacement for the linear model, I can use the exact same unsupervised genetic algorithm to train it. I appreciate that with this many parameters, unsupervised learning is not the most efficient machine learning technique, as a lot of compute is required to traverse such a large search space, but I thought it was worth a shot anyway. Maybe I will get lucky...

At this point, I made a tweak to the genetic algorithm to stop rotating the seed every 100 generations and instead rotate it every 10 stale generations, where the score did not improve. The idea behind this was to prevent the model from stagnating for too long.

I can't really show how the neural network has learned like I did with the linear model, as it is effectively a black box. There are techniques I can use to visualise activation patterns in the network to maybe derive an idea of what's going on, but I haven't done that yet.

I trained this model for literally an entire weekend and boy am I glad I left it running that long! I set a limit per game of 10,000 lines and at generation 7,750, after millions of games played, billions of in-game hours, the model FINALLY hit this limit with a score of 647,931,149 points!

There was definitely a breakthrough at around generation 6,000 that allowed the model to start scoring in the hundreds of millions of points. This is amazing, but the massive lag before the breakthrough demonstrates the drawbacks of using unsupervised learning for a problem as complex as Tetris. I'm not sure of the timing, but I think it took over 30 hours to get to generation 6,000. I could have easily turned it off before then and missed out on this breakthrough.

Using the same seed that produced the 10,000 line run, I let the model play for as long as possible. It managed to play for 3 hours, clearing 10,840 lines and scoring 760,264,498 points. I recorded the playthrough and uploaded it to YouTube for your viewing pleasure 😀:

I've managed to, somewhat luckily, grind superhuman performance out of a model-free unsupervised learning technique. Where do I go from here?

You may have noticed that I have not documented any attempt to lookahead, classifying actions by their future consequences or opportunities. That doesn't mean that I did not attempt to, just that my attempts were unsuccessful.

The issue I could not solve acceptably was the sheer amount of compute required. For example, the I tetromino shape can be placed in 17 different positions on an empty board. If the next tetromino is the L shape, then there are 35 further placements to be considered... for every one of the initial 17 placements. Also, at each placement, you have to consider the held tetromino, further branching the tree. This results in an exponentially increasing number of placements to consider for each level of lookahead.

The increased compute meant that training was significantly slower. Coupled with inefficient unsupervised learning, this resulted in an unacceptable rate of convergence.

I tried to solve this by:

Pruning the tree of placements that were obviously bad. I could not remove enough of them to make a difference and the heuristics I used were not free to compute, so I think in some cases I actually made it worse.
Training the model without lookahead and then "enlightening" it with the feature once deployed. This seemed to cause the models to perform even worse than in training without lookahead enabled. My theory is that the models learned something about, or became reliant on the scales of the feature values. For example, in training the model was typically dealing with, "if I make this placement then I will create one hole", but then in deployment it might have had to deal with, "if I make this placement then I will create 10 holes".

I am not sure that lookahead is even required for a perfect Tetris strategy (one that can play forever) so it might not be worth the effort. Maybe I might still revisit this later but with some serious pruning and a way to isolate it from the current model parameters. One approach might be to provide the model with another, much more limited set of features for lookahead placements.

I can tune the model parameters to improve the performance of the model or redirect its behaviour towards something more desirable.

If you watched any of the demo video then you may have noticed some weird behaviour where I tetromino shapes are stacked up on the RHS column. This was actually an experiment gone wrong where I added the height of the RHS column as a game feature, hoping that the model would learn to slam big Tetris clears by keeping it free 😎. However, this didn't work out and the model actually learned to do the total opposite, resulting in the stacking of I tetromino on the RHS column instead ☹️. I am not sure of the evolutionary advantage that this technique provided. Maybe it had no positive or negative effects so it was never actively selected against, and it was random chance that it remained in the final model?

I could either:

Double down and give it the heights of every column, maybe then the model will derive its own features and abstractions over the hidden layers? This will probably require massive training runs with the genetic algorithm though as there will be a lot of noise to sift through.
Derive a new feature that somehow describes the behaviour I want e.g. leaving a single column open for big Tetris clears.

The genetic algorithm I am using is basically brute force on steroids.

There is no intelligence in how mutation changes the weights so no guarantee that any particular mutation will result in a better model. Maybe, via some gradient descent technique, I can bias mutation to move weights in the right direction more often? I don't know, I haven't seen anything on the internet that discusses this in depth.

There are other, much better documented, techniques available to level up the genetic algorithm. For example, I could introduce speciation to allow it to explore multiple strategies at once.

Every single game of Tetris ever played by every model I've ever trained has ended in a game over.

That must mean that the model still hasn't gotten good enough to play a perfect game of Tetris. I've not got any proof that a perfect game is possible, but I suspect that it is possible to play for much longer than 10,000 lines.

The unsupervised learning process had a massive breakthrough after many hours of training, so maybe it might make another one after a longer training run?

The models still haven't learnt the canonical strategies of master Tetris players, who tend to optimize for Tetris clears. I think the reason for this is that for any non-Tetris optimized strategy, a longer game will usually result in a higher score. So a survival orientated strategy has received a higher selection pressure over more risky techniques that may have resulted in higher scores if they were explored further.

I think I can address this by taking a survival optimized model and then either:

Training it with a supervised learning technique to optimize for Tetris clears or to mimic professional play styles.
Further training it with unsupervised learning but limit game time to force more efficient scoring strategies.

All the code for this project, and most of the failed attempts, can be found on the ai branch of Rustris. This has been a massive undertaking, so please if anyone has read this far and is interested then do check it out and give it a star ⭐.

Machine Learning From Scratch

Target

Tetris

API

State

Features

Action

Move Search

Linear Model

Agent

Linear Model Training

Supervised learning

Reinforcement learning

Unsupervised learning

Genetic algorithm

Training stability

Linear Results

Linear Coefficients

Linear Performance

Neural Network Model

Hold on, what is a neural network exactly?

Neural Network Training

Neural Results

Demo

Next Steps

A better agent

Tuning model parameters

More intelligent unsupervised learning

Longer training runs

Optimizing for Score

The Code